Vous pouvez télécharger ce cours au format pdf : Télécharger
Chapitre 9
Quelques questions réponses:
A la relecture après quelques temps de récupération de l’effort, je me suis glissé dans la peau du lecteur en essayant d’anticiper sur d’éventuelles questions.
C’est tellement plus simple de répondre aux questions quand on se les pose soi-même. ☺
Ce qui n’empêche pas de rester ouvert à de vraies questions posées par de vrais lecteurs.
Question 1 :
Dans les 7 premiers chapitres, il est toujours question de déplacements en distance.
Pourquoi les problèmes de rotation n’ont pas été abordés?
Réponse 1 :
Il y a une bonne et une mauvaise raison.
La mauvaise raison, c’est que l’étude cinématique de la rotation est infiniment plus complexe que la translation.
L’énergie mécanique d’un robot en translation correspond à son énergie cinétique égale à ½M.v². Pour un robot en rotation, son énergie cinétique vaut ½ J.w².
Toute la différence est là. La masse M, tu peux facilement l’évaluer, il suffit d’une balance. Pour le moment d’inertie J=∑ m.r² c’est un autre problème. Il n’existe pas de balance à moment d’inertie☺. Et puis le comportement dynamique du robot, si on s’intéresse aux transferts de masse devient un vrai casse-tête.
La bonne raison, car il faut bien se donner bonne conscience, c’est que les rotations dans un robot Eurobot posent beaucoup moins de problèmes que les déplacements.
Le robot se trouve placé dans un environnement hostile. Il doit contrôler en permanence des obstacles fixes (bordures, totem, bac à pile…) et un obstacle mobile (l’adversaire). La vulnérabilité du robot face à ces dangers potentiels est beaucoup plus grande en déplacement qu’en rotation. En déplacement un robot va devoir adapter sa vitesse en permanence. On n’aborde pas une bordure à la même vitesse que lorsqu’on se déplace plein champ. (Quoique pour certains…). On n’aborde pas non plus l’adversaire à sa vitesse max (Quoique pour certains…). Pour la rotation les problèmes des risques de blocage sont réduits. Si le robot est cylindrique et tourne autour de son centre, les risques sont même nuls. On pourra en conséquence adopter une valeur de vitesse angulaire unique et valable pour toute la durée du match. Idem pour l’accélération. Ce qui simplifie les problèmes de choix pour la rotation.
Question 1 :
Il est dit, diapo4, que Fx=0 quand l’accélération est nulle. Ce qui veut dire que le robot avance à vitesse constante et que la force de traction est nulle. J’en déduis que si les moteurs ne poussent plus le robot, ils ne servent plus à rien et on peut imaginer un robot à 1m/s sans moteur.
Réponse 2 :
Déjà les moteurs ont permis d’accélérer le robot à cette vitesse de 1 m/s. Ensuite dans la phase à vitesse constante, effectivement la force de traction exercée par les roues est nulle (L’équation fondamentale de la mécanique Fx=M. est incontournable) mais les moteurs doivent fournir un couple pour compenser les pertes par frottement (balais de collecteur, pignons de réducteur, roulements…) et on n’ imagine pas un robot à 1m/s sans perte.
Question 3 :
Diapo 5, à propos du coefficient d’adhérence, il est dit que sa valeur peut dépasser la limite théorique de 1. Alors les théoriciens se planteraient?
Réponse 3 :
Ca s’est déjà vu ☺, mais en l’occurrence ce n’est pas le cas. En fait la limite ka=1, s’applique à des solides indéformables. Dans le cas de pneus sur bitume ou bois peint, apparaît un phénomène d’indentation. Le pneu en contact avec le sol se déforme et s’engrène dans les rugosités du terrain, d’autant plus que le degré shore du pneu diminue. Ceci explique cela.
Question 4 :
Dans la mesure du coefficient d’adhérence par la méthode du seau suspendu, tu m’as fait peur avec cette histoire de température moteur. Si pendant que je charge le seau, je maintiens un doigt sur l’un des moteurs et si j’arrête quand ça brûle, qu’est-ce que t’en penses?
Réponse 4 :
J’en pense que tu vas commettre une erreur fatale. La constante de temps thermique de la carcasse de quelques 700s va restée froide alors que la température du rotor peut dépasser 110 °C et ton rotor peut partir en fumée. (Ton moteur peut griller en restant froid! ).
La sécurité dans cette manip c’est de bloquer mécaniquement les roues.
Question 5 :
En diapo 26, il est dit que la puissance mécanique que peut fournir le moteur est maximum quand la tension Vcc se partage également sur les 2 termes ohmique et vitesse. D’où ça sort et quel rapport avec la puissance nominale donnée pour le moteur
Réponse 5 :
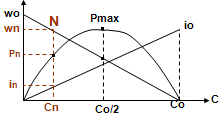
Vcc=r.i + λv.w (1)
C=λc.i (2)
Pm=C.w (3) représente la puissance fournie par le moteur
Des équations 1, 2 et 3 tu déduis
Pm=Vcc.C – (r/λc).C²
Le maximum de Pm en fonction de C s’obtient pour dPm/dC=0 soit après dérivation:
C= ½ λc.Vcc/r = ½ λc .io = ½ Co
io représentant le courant de démarrage et Co le couple de démarrage
Le maxi de Pm correspond donc à C = ½Co et w = ½wo, ce qui prouve que les termes r.i et λv.w sont égaux (Vcc se partage également sur les 2 termes) et
Pmax = ¼ Co.wo (Co couple de démarrage, wo tension à vide)
Si on prends l’exemple du moteur RE025 en 24v, ça donne:
Co=241mNm
wo=9550tr/mn=1000rd/s
Pmax=60w à comparer à la puissance nominale donnée pour 20w
La puissance nominale Pn est donnée comme une puissance en régime permanent supportable en terme de température rotor. Elle correspond aux valeurs rouges sur le graphe et on est bien en dessous de la puissance max.
Question 6 :
C’est quoi cette histoire de λc=λv. T’es sûr de toi?
Réponse 6 :
J’ai pris plusieurs exemple de moteurs et ça colle au poil. C’est tellement vrai que ça doit se démontrer mais là j’avoue mon incompétence. Tout au plus quelques réminiscences des temps anciens et là je fais appel à ma mémoire reptilienne et quelques vieilles formules reviennent à la surface comme:
e= d(FLUX)/dt et C=FLUX.i
FLUX : Flux magnétique créé par un champ magnétique B
e: fem induite par une variation du FLUX qu’on pourrait écrire e=FLUX.w
C: couple induit par la force de Laplace.
Si on compare C=λc.i à C=FLUX.i et e=λv.w à e=FLUX.w
ça semblerait coller et montrer que finalement
λc et λv seraient homogènes à un FLUX magnétique. (Celui créé par les aimants du stator)
L’unité de FLUX étant le Weber qui s’exprime en [v].[s] , pour λv qui s’exprime en V/rd/s ça semble coller.
Pour λc, c’est moins évident mais finalement j’ai bien vérifié que des N.m/A donne des [v].[s]
Question 5 bis :
Mais alors ça sert à quoi d’avoir 2 coefficients?
Réponse 5 bis :
Je pense que c’est pour des raisons pratiques. Quand tu raisonnes sur le couple il vaut mieux utiliser λc qui fournit des N.m. quand tu raisonnes sur la vitesse, il vaut mieux utiliser λv qui fournit une tension en volts pour une vitesse donnée en rd/s.
Question 7 :
Dans les diverses formules, apparaît toujours la tension batterie Vcc. Normalement elle doit être égale à la tension nominale du moteur ? Non?
Réponse 7 :
C’est quasiment impossible d’avoir une tension batterie égale à la tension nominale du moteur. Tout au plus, on peut essayer de s’en approcher.
Pour une batterie LIPO, chaque élément fourni une tension 3.7v en moyenne et 4.2v en pleine charge (sortie du chargeur) et la tension batterie sera un multiple de cette valeur.
Pour un moteur 24v: 6 éléments LIPO donnent 22v moyen et 25.2v max
7 éléments LIPO donnent 26v moyen et 29.4v max
Pour du NiMH, c’est le même problème avec des variations importantes de la tension suivant l’état de charge.
Si on part du principe qu’avant chaque match, on part avec une batterie à bloc, on connaît alors la tension batterie Vcc effective ( 25.2v avec une batterie LIPO à 6 éléments par exemple).
Ce qu’il faut savoir c’est que dépasser la tension nominale du moteur est parfaitement possible à condition de ne pas exagérer.
Il existe 2 causes de destruction d’un moteur:
à Dépassement de la température rotor autorisée: destruction du rotor par échauffement
à Dépassement de la vitesse angulaire autorisée: destruction du rotor par surrégime.
Si la tension batterie dépasse trop la valeur nominale, on risque dans les 2 cas.
Le risque par échauffement est limité si on respecte les conditions de ce document en particulier la condition de glissement en cas de blocage.
Par contre, un surrégime est toujours possible en cas de bug logiciel car alors toute la tension batterie peut être appliquée au moteur et celui-ci risque fort de passer en surrégime.
Question 9 :
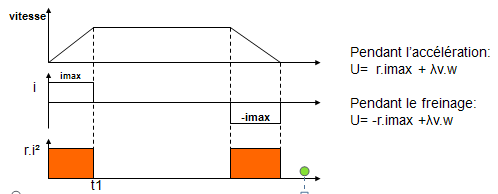
J’ai l’impression que c’est pendant l’accélération que le moteur chauffe le plus car alors la commande U appliquée au moteur est la plus forte.
Réponse 9 :
Le moteur chauffe autant pendant le freinage que pendant l’accélération.
En valeur absolue si les accélération sont égales, les couples sont égaux donc les courants sont égaux.
Donc effectivement la tension U est plus grande pendant l’accélération mais l’énergie thermique dépensée égale à r.i².t1 (aire en rouge) est la même pendant accélération et freinage.
Question 10 :
Si j’ai bien compris, la diapo 40, pour un moto réducteur donné, le choix de l’accélération et de la vitesse max correspondante se fait en fonction de l’équation:
vmax = vo .(1– γ max/γ o)
Donc si j’augmente l’accélération, je dois diminuer la vitesse max correspondante.
Réponse 10 :
T’as bien compris.
Question 11 :
Et comment je choisis ce couple de valeurs. Laquelle de ces 2 grandeurs faut-il favoriser?
Réponse 11:
Tout dépend de la distance à parcourir.
Pour les courts trajets, on a intérêt à avoir une accélération forte (inférieure bien sûr à l’accélération max qui déclenche le glissement ou le weeling).
Pour les longs trajets (une traversée du terrain par exemple), on a intérêt à avoir une vitesse forte.
On peut imaginer d’optimiser par logiciel l’accélération et la vitesse max en fonction de la distance à parcourir. Ce n’est pas compliqué à écrire.
Question 12:
Je résume. J’ai choisi mon moteur et réducteur afin d’avoir un couple suffisant pour déclencher un glissement en cas de blocage.
J’ai choisi ensuite vitesse max et accélération afin d’éviter la saturation des amplis tout en m’assurant, en fonctionnement sans blocage, que l’accélération ne déclenche ni glisse ni weeling.
Mais étant donné que les moteurs chauffent pendant accélération et freinage, qui me prouve que même si les conditions ci-dessus sont respectées, les moteurs ne vont pas dépasser leur température autorisée en 1mn30 de match. Et je pourrais poser la même question pour les amplis de puissance.
Réponse 12:
Aparté: La perfidité de l’auteur ne vous aura pas échappé. Vous avez tous compris que si je me pose cette question c’est que j’y ai réfléchi et que je pense pouvoir y répondre. Ma réponse pourrait être dans un 1er temps, histoire de vous montrer que je sais aussi manier l’humour à 3 balles: ☺
Tu veux peut-être aussi l’âge du capitaine?
Et pourquoi pas histoire de me donner de l’importance: ☺
Ta question est complexe mais très intéressante. On va essayer d’y répondre.
Le coté humilité de la réplique, dans le « On va essayer… », ne vous aurait pas trompé.☺
La réponse:
La température prise par les moteurs et amplis de puissance sur la durée d’un match va dépendre du facteur de marche. A motorisation et poids de robot égal, un robot hyper actif va chauffer davantage qu’un robot qui se promène. Mais on peut toujours envisager le pire des cas.
Le plus simple pour répondre à la question est de faire un bilan énergétique:
En cours de fonctionnement du robot, s’établissent des échanges entre énergie électrique, énergie thermique et énergie mécanique.
L’énergie électrique Ee est fournie par la batterie. L’énergie thermique Ej est dissipée par effet joule dans les moteurs et amplis de puissance et aussi par frottements. L’énergie mécanique Ec correspond à l’énergie cinétique du robot.
Phase accélération: La batterie fournit une énergie qui produit de l’énergie cinétique au robot avec des pertes par effet joule.
Ee= Ej + Ec
Phase freinage: Le robot restitue son énergie cinétique qui s’ajoute à une éventuelle contribution Ee de la batterie. Le tout est dissipée en chaleur dans les moteurs et les amplis.
Ec+Ee = Ej
Phase à vitesse constante: La batterie fournit une énergie pour compenser les pertes par effet joule essentiellement les frottements.
Ee=Ej
Robot à l’arrêt:
Ee=EJ=Ec=0
Bilan pendant la phase accélération:
A la fin de l’accélération, le robot a acquis une énergie cinétique:
Ec=½ M.vmax²
Remarquer que cette énergie acquise ne dépend pas de l’accélération c’est à dire du temps qu’a mis le robot pour atteindre cette vitesse.
Exemple:
M =14 kg
K =20 rapport du réducteur
r =2.34ohm résistance d’induit des moteurs
λc =23.5 mNm constante de couple
D=6cm Diamètre des roues motrices
vit_max=1.2 m/s
acc=0.4g
Ec=½ *14*1.2²= 10 joules soit l’équivalent de 2.4 calories
Ca peut paraître ridicule comparé à votre ration quotidienne de 2000c que vous ingurgitez sous la forme de pizzas ou autres saloperies, bande de goinfres.
Mais calculons le temps mis par le robot pour atteindre cette vitesse:
t1= vit_max/acc = 0.3s
Ce qui correspond à une puissance mécanique moyenne pendant la phase accélération:
Pm = Ec / t1 = 33 w
Ca paraît déja plus raisonnable.
Calculons l’énergie thermique dissipée dans les moteurs. Comme l’accélération est constante, le couple donc le courant le sont aussi. Compte tenu des données, le calcul du courant d’induit moteur donne: (2Fx=M.acc; Cr= Fx.D/2; Cm=Cr/(K.Rd); i= Cm/ λc )
i= 2.5A courant d’induit par moteur
Ej1=2.r.i².t1= 8.8 j énergie dissipée par effet joule dans les 2 moteurs
Il faut ajouter l’énergie perdue dans les amplis de puissance (Pour LM18200 ra=0.6ohm)
Ej2=2.ra. i².t1= 2.25 j
Ej1 + Ej2 = 11 j énergie totale perdue par effet joule
Soit l’énergie électrique fournit par la batterie (On néglige les frottements)
Ee=Ec+Ej1+Ej2= 21 j
Au total à chaque accélération la batterie fournit 21j, dont 10j mécaniques utiles pour propulser le robot à sa vitesse max et 11j perdus par effet joule.
Phase freinage
On a vu que les pertes dans les moteurs sont identiques à l’accélération et au freinage. Soit
Ej1= 8.8j perdus par effet joule dans les moteurs.
Admettons qu’il en est de même pour les amplis
Ej2=2.25j
Soit au total, une énergie perdue par effet joule:
Ej1 + Ej2 = 11j
Le robot fournit une énergie mécanique égale à son énergie cinétique perdue:
Ec= 10j
Cette énergie est dissipée dans moteurs et amplis de puissance.
11j perdu pour 10j fourni . Donc la batterie fournit le complément soit 1j
Ee+Ec= Ej1 + Ej2
Au total à chaque freinage, le robot fournit 10j, la batterie fournit 1j
8.8j sont perdus par effet joule dans les moteurs et 2.25j perdus dans les amplis.
Pendant la phase à vitesse constante, les pertes par effet joule sont négligeables.
Le bilan total d’une séquence accélération freinage conduit donc à:
Séquence accélération freinage
Ej1= 2*8.8 = 17.6j perdus par effet joule dans les moteurs
Ej2= 2*2.25 = 5.5j perdus par effet joule dans les amplis
Ee = 21+1 = 22j fournis par la batterie.
Revenons à la question de connaître la température des moteurs après 1mn30 de match.
Elle va dépendre du facteur de marche:
Prenons un cas extrême d’un robot jamais à l’arrêt avec une suite de déplacements de 40cm ce qui donne avec notre exemple un facteur de marche de 2/3.
(0.6s pour accélérer et freiner sur 0.9s au total pour le déplacement de 40cm)
Soit:
Pj1 = Ej1/0.9 = 20 w environ de puissance moyenne dissipée dans les 2 moteurs
Pj2 = Ej2/0.9 = 6 w environ de puissance moyenne dissipée dans les amplis
Donc la puissance moyenne dissipée dans chaque moteur vaut:
Pj=10w
Reprenons les constantes thermiques du moteur:
Rthr = 3°C/w résistance thermique rotor-stator
Rths= 10°C/w résistance thermique stator-ambiant
Constante de temps rotor = 20s
Constante de temps stator= 700s
Elévation de la température du stator:
Pj.Rths = 10*10 = 100°C écart de température asymptotique entre stator et ambiant.
Du fait de la constante de temps stator de 700s et en approximant exponentielle et tangente ça donne après 90s de match:
Ts – Ta = 100* 90/700= 13°C
Avec Ta= 40°C (température Ferté en finale☺)
Ts= 53°C
Elévation de température du rotor
Tr–Ts = Pj.Rthr = 10*3 = 30°C écart de température asymptotique entre rotor et stator
Cet écart sera atteint après 20s de match environ soit en fin de match:
Tr= 30 + 53= 83°C
Question 13:
L’erreur de traînage, écart entre la vitesse et sa consigne qu’on peut constater sur les relevés graphiques n’est-elle pas gênante pour la précision de l’asservissement.
Réponse 13:
Dans la phase à vitesse constante, la vitesse est égale à sa valeur de consigne. C’est déjà un premier point. Pendant les phases accélération et freinage la vitesse est effectivement en retard sur la consigne mais ça n’a pas d’ incidence sur la précision du robot.C’est la distance qui nous intéresse, ce qui justifie le choix d’un asservissement en position. La vitesse n’a d’incidence sur les performances du robot que par le biais du contrôle dérivé du correcteur.
Par contre pendant accélération et freinage la distance est aussi en retard sur sa consigne et il faut en tenir compte dans la condition de sortie des fonctions déplacement. Quand la consigne est atteinte, le robot est encore en mouvement.
Question 14:
Sur les relevés graphiques, je suis surpris par le niveau de bruit sur la commande des moteurs et aussi à un degré moindre sur la vitesse.
Réponse 14:
Ce qui pourrait être préoccupant c’est le bruit sur la vitesse. Mais en fait il ne s’agit pas de la vitesse, il s’agit d’une mesure de la vitesse par un algorithme simpliste:
vitesse(n)=distance(n) – distance(n-1).
Ce qu’on observe est lié au bruit de quantification, et on peut imaginer que la vitesse réelle du robot du fait de la constante de temps mécanique n’est pas soumise à ces fluctuations.
On peut d’ailleurs réduire ce bruit en sous échantillonnant la vitesse à l’ordre k:
vitesse(n)=distance(n) – distance(n-k).
Mais il ne faut pas exagérer sur la valeur de k. Trop c’est trop et ça risque de
dégrader le rôle prédicteur du correcteur dérivé. On ne prédit pas l’avenir en remontant trop loin dans le passé. S’il est 17h et qu’on cherche à prévoir la météo pour 18h, on ne va pas chercher les conditions météorologiques d’il y a 3 jours mais plutôt celles de 16h.
Il est vrai que si le bruit de vitesse n’a pas d’incidence sur le comportement de l’asservissement, il faut être plus réservé par rapport à l’odométrie. Mais le sujet n’est pas abordé dans ce document.
Question 15:
Tu nous as rien dit sur la manière de régler le correcteur. Apparemment vous travaillez sur des relevés graphiques. Et si je ne dispose pas de l’outil correspondant, comment je procède.
Réponse 15:
Un conseil: Si tu ne disposes pas de debuger, fabrique le. Il y a des outils très simples à développer qui t’apporteront une aide précieuse voir indispensable au cours de ta phase de mise au point (normalement la phase la plus longue sur la durée du projet).
Sans visualisation graphique, il y a toujours un moyen de t’en sortir mais ça risque d’être moins précis.
Quant à la procédure de réglage, elle a été largement évoquée sur le forum.
En gros, on dégrossit l’asservissement en commande proportionnelle puis on introduit le terme dérivé. Et pour les inconditionnels, on finit par le terme intégral.
Bien sûr en asservissement polaire, on décompose en réglant d’abord un paramètre puis l’autre. C’est mieux de commencer par l’orientation .
Une des difficultés réside dans le fait que pour régler l’asservissement avec précision, il faut faire bouger le robot donc avoir écrit les séquences de rotation et de déplacement en ligne droite. Or pour mettre au point ces séquences, il faut que l’asservissement soit à peu près réglé. Donc on tourne en rond.
Voilà un moyen très simple de s’en sortir:
Le plus simple des déplacements, c’est l’absence de déplacement.
Dans un 1er temps, on va régler le correcteur en asservissant le robot sur une position fixe.
Pas de profil trapézoïdal à programmer mais simplement asservir le robot sur
consigne_distance=0.
Le principe est d’imposer une condition initiale non nulle à l’asservissement et d’observer pour t>0, le retour du robot vers sa position d’équilibre.
A: Réglage de l’asservissement en rotation (commande_distance=0)
- On se met en commande proportionnelle (kd=0)
On part d’une valeur kp à priori faible et on vérifie la stabilité de l’asservissement en essayant d’écarter le robot de sa position d’équilibre et en relâchant la pression. Le robot doit tranquillement revenir à sa position d’équilibre.
Puis on augmente progressivement le gain proportionnel kp.
On voit d’abord apparaître un retour à l’équilibre oscillatoire amorti.
On continue à augmenter le gain jusqu’à l’oscillation amortie sur 1 à 2s. On est alors juste avant la limite de l’oscillateur.
(Sur notre robot, on trouve kp= 0.35)
- On introduit le terme dérivé.
On augmente progressivement le gain dérivé kd, toujours avec le même procédé.
On passe d’abord par une phase en retour oscillatoire amorti puis par un parfait retour apériodique sans dépassement.
(Sur notre robot, on trouve kd=2)
On peut considérer que l’asservissement en rotation est largement dégrossi.
B: Réglage de l’asservissement en distance
Le robot étant asservi en rotation, on introduit la commande distance qui a été annulée
précédemment.
La procédure est la même que pour l’asservissement en orientation
- On se met en commande proportionnelle (kd=0)
On augmente kp jusqu’à la limite de l’oscillation maintenue. L’oscillation doit être
amortie sur un temps de l’ordre de 1s à 2s environ.
(Sur notre robot, on trouve kp=0.5)
- On introduit le terme dérivé, et on augmente kdjusqu’au retour impeccable sans
dépassement.
(Sur notre robot on trouve kd=4)
On peut considérer à ce stade que notre correcteur proportionnel et dérivé est dégrossi.
Remarque générale sur cette méthode de réglage:
Elle permet de dégrossir les réglages avant d’avoir mis au point les séquences de déplacement.
Certains pourront critiquer son caractère sauvage. Ils n’ont pas tord. Car on doit forcer le robot à quitter sa position d’équilibre puis tout lâcher.
On retombe sur le problème de blocage du robot évoqué dans un chapitre précédent et le robot va s’opposer farouchement au méchant perturbateur. Sa force de réaction augmente avec la valeur de kp et aussi avec l’amplitude du décalage par rapport à sa position d’origine.
Au-delà d’une certaine amplitude de décalage, le glissement des roues risque d’apparaître.
Mais il est conseillé de ne pas exagérer sur les amplitudes. Par exemple:
5 à 10 degrés pour la rotation
5 cm pour la distance
Si cette méthode inquiète, il est possible de procéder d’une manière plus soft:
Elle consiste à lancer le programme sans valider la puissance des moteurs
On écarte le robot de sa position initiale sans la puissance (Le robot n’oppose aucune résistance cette fois). Le retour à la position d’équilibre va se faire dès validation de la puissance.
Cette méthode ne permettant que d’approcher les gains optimums, on peut chercher à l’améliorer:
En partant du couple de valeurs kp et kd déterminé dans un 1er temps, on augmente kp, par exemple de 20% et on cherche à récupérer la stabilité en augmentant kd. Et ainsi de suite jusqu’au moment ou le terme dérivé ne peut plus récupérer la stabilité.
Mais ne pas trop en faire par cette méthode qui doit rester une méthode de 1ere approche.
Si on veut finaliser ces valeurs, il faut ensuite introduire des déplacements en rotation et distance avec consignes trapézoïdales classiques, ce qui suppose bien sûr que ces fonctions soient parfaitement mises au point avec en particulier un freinage bien maîtrisé. C’est là que la visualisation graphique apporte un avantage certain. Mais attention à ne pas imputer au correcteur d’asservissement des défauts de comportement qui pourraient provenir d’une mauvaise programmation de la séquence des consignes.
