Vous pouvez télécharger ce cours au format pdf : Télécharger
Chapitre 3
Choix d’un profil de vitesse
On va définir un profil de vitesse pour les phases accélération et freinage du robot en tenant compte de l’accélération maximum déterminée au chapitre précédent.
Les profils retenus pour les variables accélération, vitesse, distance sont des profils souhaités qui serviront de consigne lorsqu’on abordera le problème de l’asservissement de position.
Pourquoi un profil trapézoïdal de vitesse?
On va présenter le problème pour un mouvement de translation, sachant que les résultats obtenus seront transposables pour la rotation.
Il s’agit de déplacer le robot depuis une position d’arrêt vers un point destination par une trajectoire rectiligne et le plus rapidement possible. (On suppose qu’en position initiale, le robot est déjà positionné vers la cible).
Le mouvement va se décomposer en une phase d’accélération, une phase de freinage et le plus souvent une phase à vitesse constante.
Choix des phases accélération et freinage :
Si on veut optimiser ces phases, le robot doit être à tout instant à sa limite de patinage ou de weeling . Naturellement on gardera toutefois une marge de sécurité par rapport aux valeurs d’accélération maximum.
(Par exemple γ=0.8γmax)
Ces 2 phases imposent donc une accélération constante et le mouvement du robot devient tout simplement le classique mouvement appelé : mouvement uniformément accéléré, dont on rappelle les formules de base:
γ=constante
vitesse= γ.t
distance=½. γ.t²
Choix de la vitesse max
Il s’agit d’un problème de bon sens connaissant les dimensions du terrain et en tenant compte des missions à accomplir en présence d’un adversaire qu’il faut éviter à tout prix.
Chacun à sa vision du problème, mais il apparaît que des vitesses max de l’ordre de 1m/s constituent un choix raisonnable, sachant qu’augmenter cette vitesse au-delà va procurer un gain en temps
négligeable compte tenu des courtes distances de déplacement .
Exemple:
déplacement= 1m
γ=0.2g=2m/s² (accélération et freinage)
On appelle t1,t2,t3 la durée de chacune des 3 phases:accélération,vitesse constante,freinage.
d1,d2,d3 la distance de chacune des 3 phases.
En passant de 1m/s à 1.4 m/s on gagne 1/10 sec ce qui est négligeable!
| vmax=1m/s t1=t3=vmax/γ=0.5s (phase accélération ou freinage) d1=d3=1/2γ t²=0.25m d2=déplacement-2.d1=0.5m t2=d2/vmax=0.5s (phase vitesse constante) t1+t2+t3=1.5s |
vmax=1.4m/s t1=t3=vmax/γ=0.7s (accélération ou freinage) d1=d3=1/2 γt²=0.49m d2=déplacement-2.d1=2 cm t2=d2/vmax=0.014s (phase vitesse constante) t1+t2+t3=1.41s |
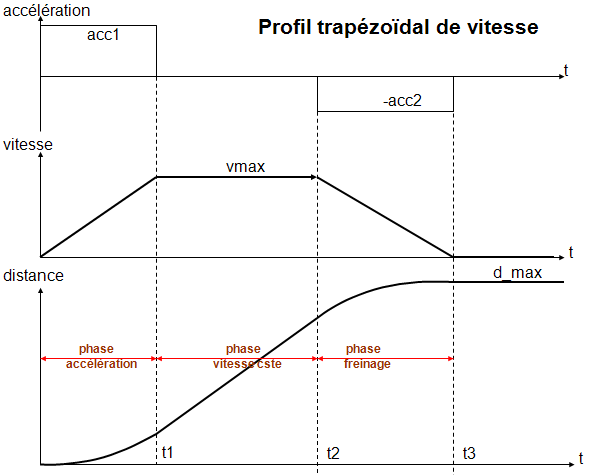
Commentaires sur le profil trapézoïdal
On note l’évolution parabolique de la distance au cours des 2 phases accélération et freinage qui permet des mouvements en douceur bien que l’accélération soit optimisée à sa limite max acceptable. Dans ces conditions, on ne voit aucun intérêt à adoucir davantage. On y perdrait en performance sans rien gagner en fiabilité mécanique.
D’autant plus qu’on verra plus tard que cette courbe de distance représente en fait une courbe de consigne de la distance. Et la constante de temps mécanique du robot va encore lisser, s’il en était besoin, l’évolution réelle du robot.
